|
Σύντομη βιογραφία του Παϊζάκη Π. |
Κριτικές του άρθρου |
Moving Object
Detection using Gaussian Mixture Model
Ανίχνευση
κινούμενων αντικειμένων με την χρήση του Γκαουσσιανού Μοντέλου
Paizakis P
Παϊζάκης Π.
Abstract
Many applications as video surveillance, optical motion capture,
multimedia application, video object segmentation, video coding, need in the
first step to detect the moving objects in the scene. So, the basic operation
needed is the separation of the moving objects called foreground from the
static information called the background. The process mainly used is the
background subtraction. In the literature, many background subtraction methods
can be found to be robust to the critical situations met in video sequence.
These different methods are classified following the model used: Basic
Background Modeling, Statistical Background Modeling and Background Estimation.
In this paper we implemented and we present the results of the Gaussian mixture
Model (GMM), a statistical background modelling. Background Representation is modelled using a
Mixture of Gaussians. Statistical variables are used in the foreground
detection to classify the pixels as foreground or background.
Περίληψη
Πολλές εφαρμογές,
όπως παρακολούθηση βίντεο, οπτική σύλληψη κίνησης, τμηματοποίηση αντικειμένων
κωδικοποίηση βίντεο, ως πρώτο βήμα απαιτείται η ανίχνευση κινούμενων
αντικειμένων στην σκηνή. Η κυριότερη διεργασία στην ανίχνευση κίνησης είναι ο
διαχωρισμός κινούμενων αντικειμένων από την στατική πληροφορία, η οποία
αναφέρεται ως υπόβαθρο. Στην βιβλιογραφία υπάρχουν πολλοί μέθοδοι αφαίρεσης
υποβάθρου και ταξινομούνται σε τρεις κατηγορίες: Βασικά Μοντέλα υποβάθρου,
Στατιστικά Μοντέλα υποβάθρου και μοντέλα εκτίμησης υποβάθρου. Στην εργασία αυτή υλοποιήθηκε και
παρουσιάζεται το Γκαουσσιανό στατιστικό μοντέλο όπου το υπόβαθρο
μοντελοποιείται κάνοντας χρήση μειγμάτων Γκαουσσιανών. Στατιστικές μεταβλητές
χρησιμοποιούνται για την ανίχνευση το προσκηνίου.
- Introduction
In
computer vision a background model refers to an estimated image or the
statistics of the background of a scene which an image or video sequence
depicts. In object tracking from video sequences, i.e. tracking people, cars,
etc., the background model plays a crucial role in separating the foreground
from the background.
The
simplest form of background model is perhaps taking an image of the scene when
no objects are present and then using that image as the background model. The
foreground can be determined by frame differencing, i.e. comparing each pixel
in the currently sampled frame to the background image and if the difference is
below some threshold, the pixel is classified as background. Such a solution
may be sufficient in a controlled environment, but in an arbitrary environment
such as outdoor scenes, light conditions will vary over time. Also, it may be
either difficult or impossible to be able to take an image of the scene without
any objects present. It is therefore highly desirable to have a background
model that adapts to the scene regardless of its initial state.
This
paper focuses on adaptive background models
that can be maintained in real-time. In some literature the adaptive methods
explained here are referred to as recursive techniques, since the current
background model is recursively updated in each iteration.
- Related Work
Background
subtraction is particularly a commonly used technique for motion segmentation
in static scenes. It attempts to detect moving regions by subtracting the
current image pixel-by-pixel from a reference background image that is created
by averaging images over time. The pixels where the difference is above a
threshold are classified as foreground. The reference background is updated
with new images over time to adapt to dynamic scene changes.
In
[11] Heikkila and Silven a pixel at
location (x, y) in the current image It is marked as foreground if
is
satisfied where 
is a predefined threshold. The background
image BT is updated as follows
Toyama et al. [3] propose a three component system for background
maintenance, (Wallflower algorithm): the pixel-level
component which performs Wiener filtering, the region-level component, fills in homogenous regions of foreground
objects and the frame-level component
for sudden, global changes. Two auto-regressive background models are used,
along with a background threshold.
Halevi and Weinshall [7] present an
approach to the tracking of very non rigid patterns of motion, such as water
flowing down a stream. The algorithm based on a “disturbance map”, which is
obtained by linearly subtracting the temporal average of the previous frames
from the new frame. Every local motion creates a disturbance having the form of
a wave, with a “head” at the present position of the motion and a historical
“tail” that indicates the previous locations of that motion. The algorithm is
very fast and can be performed in real-time.
Wren et al. [4], Pfinder models the
background using a single Gaussian distribution and uses a multi-class statistical model for the tracked object; uses a simple
scheme, where background pixels are modelled by a single value and foreground
pixels are modeled by a mean and covariance, which are updated recursively.
Haritaoglu et al. [2] propose a real time visual
surveillance system, W4, for detecting and tracking multiple people and
monitoring their activities in an outdoor environment. The system can identify
and segment the objects that are carried by people and can track both objects
and people separately. The W4 system uses a statistical background model where each pixel is represented with
its minimum (M) and maximum (N) intensity values and maximum intensity
difference (D) between any consecutive frames observed during initial training
period where the scene contains no moving objects. A pixel in the current frame
It is classified as foreground if it satisfies:
or 
The
statistics of the background pixels that belong to the non-moving regions of
current frame are updated with new image data.
- Gaussian Mixture Method
Background subtraction is a convenient and effective
method for detecting moving foreground objects in the scene. A reliable
background image is important for foreground segmentation. The pixel-based
background subtraction method basically involves subtraction of a considered
image from a reference image.
Although background
subtracting approach is simple, it may be impractical in some real applications
because backgrounds can change over time in some cases. Lighting can change the
background subtly or the camera position may drift. An alternative approach is
to find a way of adapting the background slowly such that changing background
can be characterized in real-time. Such an approach is called adaptive
background mixture models.
In our work, we implemented Stauffer and Grimson’s
algorithm [1] for background modelling. The Gaussian mixture model
representation of the scene statistics has proven to be very flexible and
reasonably efficient when implemented.
Their approach is to use mixture
models to represent the statistics of the scene. Mixture models allows a
multi-modal background model which can be very useful in removing repetitive
motion, e.g. leaves on a branch, a swaying flag or shimmering water. The method
is quite flexible and here we present the mathematical theory.
The pixel value measured by the
camera sensor is the radiance emitted from the surface point of first object to
intersect that pixel’s optical ray. In a dynamically changing scene, with
moving objects, the observed pixel value
depends on the surface
of the possible intersecting objects as well as noise introduced by the camera.
- Stauffer and Grimsons algorithm
In this
model, the values of an individual pixel (e. g. scalars for gray values or
vectors for color images) over time is considered as a “pixel process” and the
recent history of each pixel, {X1, . . . ,Xt}, is modeled by a mixture of K
Gaussian distributions. The probability of observing current pixel value then
becomes
(1)
where wi,t is an estimate of the weight (what portion of
the data is accounted for this Gaussian) of the ith Gaussian Gi,t in the mixture at time t, 
is the
mean value of Gi,t and 
is the covariance
matrix of 
and 
is a Gaussian probability
density function:
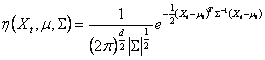(2)
Decision
on K depends on the available memory and computational power.
Also, the
covariance matrix is assumed to be of the following form for computational
efficiency:
(3)
which
assumes that red, green, blue color components are independent and have the
same variance.
The
procedure for detecting foreground pixels is as follows. At the beginning of
the system, the K Gaussian distributions for a pixel are initialized with
predefined mean, high variance and low prior weight. When a new pixel is observed
in the image sequence, to determine its type, its RGB vector is checked against
the K Gaussians, until a match is found. A match is defined as a pixel value
within (L=2.5) standard deviation of a distribution.
(4)
Next, the prior weights of the K distributions
at time t,
, are updated as follows:
(5)
Where 
is the learning rate
and Mk,t is 1 for the matching Gaussian distribution and 0 for the remaining
distributions. After this step the prior weights of the distributions are
normalized and the parameters of the matching Gaussian are updated with the new
observation as follows:
(6)
(7)
where
(8)
If no
match is found for the new observed pixel, the Gaussian distribution with the
least probability is replace with a new distribution with the current pixel
value as its mean value, an initially high variance and low prior weight.
In
order to detect the type (foreground or background) of the new pixel, the K
Gaussian distributions are sorted by the value of
.
This ordered list of distributions reflect the most probable backgrounds from top
to bottom since by Equation (5) a background pixel processes make the corresponding
Gaussian distribution have larger prior weight and less variance. Then the
first B distributions are chosen as the background model, where
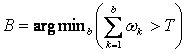(9)
and T is
the minimum portion of the pixel data that should be accounted for by the
background. If a small value is chosen for T, the background is generally
unimodal.
- Analysis of parameter values
The
Gaussian mixture models are a type of density models which are composed of a
number of components. These functions can be used to model the colours of
objects or backgrounds in a scene.
Adaptive Gaussian distributions are applicable for modelling changes,
especially when related to fast moving objects.
Threshold T is to define the fraction between
background distribution and foreground distribution. This value is based on the
background scene and the number of components in the Gaussian Mixture Model. A
small value of T (e.g T=0.1), will lead to a situation in which not all
background distribution is covered; a large T value (T=0.9) will lead to a
situation in which the foreground distribution is merging with the background
distribution. In our
thesis we use T=0.9 and change it observing different results.
K
denotes the number of components in a Gaussian mixture model. For simple
indoor scenes, a small value of K is sufficient, e.g K=2. For outdoor complex
scenes, a larger K is needed, usually 3, 4,
There are two learning rates defined
in [1]: one is the predefined learning rate
, the
other is the calculated learning rate
, which is used as a second filter in [1]. But using 
as a second learning
rate is not helpful. If we assume that the computation time of using one
learning rate α is m
seconds, the computation time of using two learning rates and was greater than 2m
seconds. For computation reasons, we used the same learning rate,
.
How
to assign a reasonable value to will depend on the given background scenery. A slowly changing
background scene needs a small learning rate; a fast changing background scene
needs a larger learning rate.
Learning rate show the speed of update. In our thesis we use
different values of (
)
with best results using
.
There is an initialization procedure
when starting the surveillance system. Assigning different initial values in
this procedure will affect the extraction of foreground regions. There are two
values that need initial consideration: mean and standard deviation. Regarding
the mean value, from our testing sequences we conclude that assigning either a
very large value or a very small value can be considered to be of benefit. In
our tests for initial mean we used
.
In the initialization procedure, we assign the
value 
to the standard
deviation based in our experiments. For standard deviation equal to zero, many
background pixels are misclassified as foreground region. In general, using
very small value of the standard deviation causes that background pixels
classified as foreground distribution.
- Implementation
Issues
We tested the computational performance and
detection quality of a moving object detection algorithm, Gaussian Mixture
Model [1]. We used sample indoor and outdoor video clips. We used as input
images 3 different video sequences on both algorithms. We used two video
sequences (winter.avi and Norwayhighway.avi) from highways with more than one
moving object. Besides we tested our algorithms at a video sequence with less
complex background; the moving object is one or two men and the background is
simpler. We implemented the Gaussian
Mixture Model using Matlab 2007b, RADtools for video analysis on
Microsoft Windows XP professional operating system
on a computer Intel core Duo and 2048 MB of RAM. The time performance analysis,
which is the per-frame processing time of these algorithms for an image size of
320x240 pixels, is shown in Table 1.
|
Detection Algorithm |
Average time to process a frame |
|
Adaptive Background Mixture Model |
12 msec |
Table 1 Performance of object detection algorithms
Figure 1
shows the flow chart of the Gaussian mixture model process. Five different
video sequences tested using Gaussian Mixture Model and the results are illustrated
in Figures 2 to 6. Figures 2 and 3 are being taken from two different highways
and the parameters that have been used are illustrated in table 2. We used
video sequences of 100 image frames for each one. We commented that we got
satisfactory results.
Figure 1 The
flow chart of the Gaussian mixture model process
Original Background Moving Foreground
Figure
2 Results obtained when running the complete algorithm on a video sequence
recorded in
Original Background Moving Foreground
Figure
3 Norwayhighway.avi. Results obtained when running the complete algorithm
on a video sequence recorded in
Background Original Moving Foreground
Figure 4 Winter.avi, α=0.01, K=4 From
Left to right: Background-Original.-
Moving Foreground
Background Original Moving Foreground
Figure 5 Winter.avi α=0.9, K=4 From Left to right:
Background-Original-
Moving Foreground
frame 21
frame 40
frame 53
frame 65
frame 81
Background Original Moving Foreground
Figure 6 Twomen.avi α=0.9, K=4 From
Left to right: Background- Original-Moving
Foreground
The
algorithm detects the most moving objects. Without dispute, there are objects
that have not been detected and the reason is for these objects there is not
motion during image sequences. Furthermore, we comment that in many of the
moving objects there are shadows. Moreover, it is very important the fact that
the algorithm detects greatly the moving objects that are appeared in the scene
after some frames and we can notice it in figures 2 and 3.
In figure 3, we used a video sequence recorded at an
intersection in
In
figures 4 and 5 we make a comparison among the same image frames using
different parameters at each occasion. In figure 4 we use as learning rate α=0.01 and K=4 and in figure 5 we use as learning
rate α=0.9, and the
same number of Gaussian components, K=4.
Comparing the correspondences image frames from figures 4-5 we notice that in
figure 5 the algorithm detects more moving objects with less shadow. The
disadvantage is that in some occasions the algorithm does not detect the whole
moving object but a part of it.
Lastly,
in figure 6 (Twomen.avi) we tested the Gaussian Mixture Model at a video
sequences with less complex background. There are only two moving objects with
a stationary background. The results are adequately but we notice that in the
first frames there is noise but at the last frames we take clearly the moving
objects and without shadows.
- Results
We implemented the method reported in [1], “a
statistical adaptive Gaussian Mixture model for background subtraction”. We only chose the distribution with
the highest weight ω/σ as the background pixel value, instead of using the T criterion before
mentioned. In the experiment the variables are parameters α and Κ.
For the following tests, we used
video sequences from European intersections in
|
Background Modelling |
|
K=4 |
|
α=0.001 |
|
λ=2.5 |
|
Τ=0.9 |
|
μ=0.01 |
Table 2 Parameter
values used to generate figures 2 and 3
The advantage is that there are only two
parameters that need to be defined in advance, and they do not need to be
changed during sequence processing. Also it is a stable and robust method. It
works very well for fast moving objects in complex environments. On the other hand there are many disadvantages
using Gaussian Mixture Model.
1. The main disadvantage is that while an object
is moving very slowly, it will be treated as part of the background, or just
detected based on differences between the current frame and previous frames,
and the overlapping regions of the moving object cannot be detected as
foreground.
2. While testing a large moving object,
holes left at the overlapping regions. This occurs because a slowly moving
object has a small variance, which will match the background model, and
as a result the slowly moving object was absorbed by the background.
3. The assign of initial values to
these parameters (α, T,
K) affects the accuracy of background subtraction.
4. In case that shadows are foreground,
of the surface was covered by shadows a significant amount of the time, a
Gaussian representing those pixels values may be significant enough to be
considered background.
5. Furthermore, when an object enters
the scene it is not well detected during a few frames since the Gaussian models
have to adapt to this case.
6. Lastly, when a moving object stops,
the MGM starts to split the region until it disappears, becoming part of the
background.
- Conclusions
In this paper we present a method for background
modelling using the Gaussian Mixture Model. No object detection algorithm is
perfect, so is our method. The method which we present show promising results
and can be used as part of a real-time surveillance system or utilized as a
base for more advanced research such as activity analysis in video. Using
mixture models provides a flexible and powerful method for background
modelling.
Beside the various contributions in
the present paper, the complete framework for intelligent video analysis is
still non perfect. Many improvements could be introduced at several levels.
The
generic framework for intelligent video analysis as presented in this paper
still is uncompleted. We have explored in our research some stages of this
framework and not all the stages. The exploration of the other stages (action
recognition, semantic description, personal identification and fusion of
multiple cameras) makes the application range wider. Thus, we can consider more
advanced applications based on fusion of multiple sensors as well as a
recognition system for controlling high security areas.
Bibliography
[1]
Chris Stauffer and W.
Eric L. Grimson. Adaptive background
mixture models for real–time tracking. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recognition (CVPR), pages
II: 246–252, 1999.
[2]
[3] K. Toyama, J. Krumm, B. Brumitt and B.
Meyers: Wallflower: Principlesand practice of background maintenance in: International Conference on Computer Vision
(1999) pp. 255-261.
[4] C. Wren, A. Azabayejani, T. Darrell and A. Pentland: Pfinder: Real-time tracking of the human body IEEE Transactions on Pattern Analysis and Machine
Intelligence19 (1997) 780-785.
[5] Alan M. McIvor, Background Subtraction
Techniques, Reveal Ltd POBox 128-221, Remuera, Auckland, New Zealand.
[6] Weiming Hu, Tien-Niu Tan, Liang Wang,
and Steven J. Maybank. A survey on visual surveillance of
object motion and behaviors. IEEE Transactions on Systems, Man, and Cybernetics-Part C:
Applications and Reviews, 34(3):334– 352, 2004b.
[7] G.
Halevy and D.Weinshall: Motion of
disturbances: Detection and tracking of multibody non-rigid motion Machine Vision and Applications 11
(1999) 122-137, 1999.
[8] Jacinto
Nascimento and Jorge Marques. Performance evaluation of object
detection algorithms for video surveillance, Multimedia, IEEE
Transactions on Volume 8, Issue 4, Aug. 2006 Page(s):761 – 774, 2006.
[9] Qi
Zang and Reinhard Klette: “Parameter Analysis
for Mixture of Gaussians Model”, Department
of Computer Science,
Tamaki Campus, The University of
[10]Jacinto
C.Nascimento, Jorge S.Marques: “Novel
Metrics for PerformanceEvaluation of Object Detection
Algorithms”, IEEE
Transactions on Multimedia, (TMM):761-774, Lisboa
[11] J.Heikkila and O.Silven. A real time
system for monitoring of cyclists and pedestrians. In proc. of second
IEEE Workshop on visual Surveillance, pages 74-81,
© Copyright-VIPAPHARM. All rights reserved
